絶対に役に立つ~頭の片隅に法則を~①

○○の法則って世の中にあふれていますよね。
どんな人でも一度は聞いたことがあると思います。
かなたも色んな本を読んだりセミナーに参加したりして様々な法則や説をインプットしてきました。
必ずしも役に立つものばかりではないですが理解しておくと何かの指標になることがあります。
例えば学校で聞いたときは「これ将来何に使うの?絶対に使う事ないだろう」と思っていた「ピタゴラス(三平方)の定理」
これ建築関係ではめちゃくちゃ使います。
見た目まさに「ヤンキー」なお兄さんが普通に使ってるところを目の当たりにしたこともあります。
ちなみにこれは直角三角形の3辺のうち2辺が分かれば残りの1辺の長さが出せるってものです。
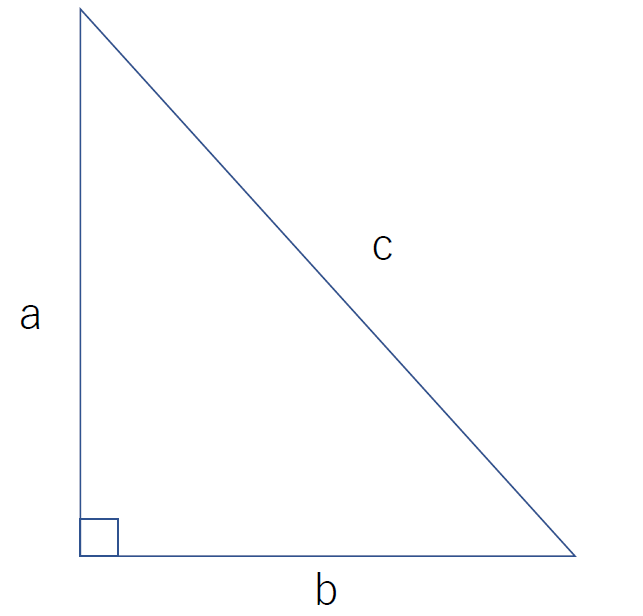
ピタゴラスの定理の公式は「a² + b² = c²(斜辺)」
例えばa=4、b=3とするならば
4²+3²=c²
16+9=c²
c²=25となり、c(斜辺)=5ということが分かります。
これにより3つの辺の比が3:4:5ならば直角三角形になるということもわかります。
だから何?と思われるかもしれませんがこれは「距離を知りたい」「直角を出したい」ときによく使われます。
例えば建物って四角形のものが多いですよね。
四角ということは四隅は基本的に直角です。何もないところからどうやって直角を出すのか考えたときこれが役に立ちます。
一生使わない人もいると思いますが・・・
例として有名な「ピタゴラスの定理」を出しましたが、この後、数学の話は一切しません(笑)
今回はかなたが「覚えてて良かった」や「あれ?これあのの法則だ」ってなった役に立った法則や説たちを紹介していこうと思います。
もくじ
パレートの法則
これは有名なんで聞いたことがあるかもしれません。
いわゆる80:20の法則です。
イタリアの経済学者パレートさんが発見したものになります。
簡単に言うと、全体の8割の事象は残りの2割が生み出しているということです(経済において)
例えば日本国民全員の月給を合計して100億円だったとします。
この100億円の8割、つまり80億円はお金持ち、いわゆる富裕層の手に渡り、富裕層以外の人たちが20億円を受け取ります。
日本人の富裕層は人口の2割、それ以外が8割。
つまり8割という大人数で20億円を稼いでいること、2割という少人数で80億円を稼いでいることが分かります。

他にも
ビジネスにおいて、売上の8割は全顧客の2割が生み出している。よって売上を伸ばすには顧客全員を対象としたサービスを行うよりも、2割の顧客に的を絞ったサービスを行うほうが効率的である。
商品の売上の8割は、全商品銘柄のうちの2割で生み出している。
売上の8割は、全従業員のうちの2割で生み出している。
仕事の成果の8割は、費やした時間全体のうちの2割の時間で生み出している。
故障の8割は、全部品のうち2割に原因がある。
住民税の8割は、全住民のうち2割の富裕層が担っている。
プログラムの処理にかかる時間の80%はコード全体の20%の部分が占める。
全体の20%が優れた設計ならば実用上80%の状況で優れた能力を発揮する。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
80:20が70:30であったり85:15であったりはしますが正確な数字が大事なのではなく殆どの事象が80:20に近い数値になるということが重要です。
(実はこのパレートの法則は提唱された当初から問題があることをパレート自身も認めていました)
それが頭に入れば「これは大体80:20だから・・・こんな感じになるかな」という風に使えば凄まじい時短に繋がることもあります(数値を1から計算しなくていいので)

働きアリの法則

これはよく講義とかでパレートの法則と一緒に使われます。
かけ離れた理論で話される方もいますが・・・
こちらは「20:60:20」で、働きアリを観察すると
良く働くアリ20:普通に働く(たまにサボる)アリ60:サボるアリ20
に分かれるというものです。
例えばこの「サボるアリ」のみを集めるとこれまた「20:60:20」に分かれて全体の80は働き始めます。
逆に「良く働くアリ」だけを集めても「20:60:20」に分かれてサボるアリが現れます。
そして取ってくる食料の8割は良く働くアリ(2割)で賄っている、といったものです。
実はこれ、サボっているのではなく組織存続のための役割分担です。
みんなが一斉にがむしゃらに働いたらそのときは最高効率をたたき出します。
でもその後は疲れ果ててしばらくは稼働も成果も「0」になりますよね。

その休憩が長ければ長いほど「0」状態も長くなり食料はどんどんなくなります。
そうなると組織は崩壊します。
「20:60:20」の視点を変えて考えると
チームリーダー20:作業員60:予備人員20 という風に見えてきます。
アリたちが生命維持、種の存続を考えたとき最も効率的で効果的だったのが「20:60:20」だったということになります。
サボっているように見えるアリも実際はいつでも出動準備ができている頼もしいサブだったんですね。
これは人間の会社組織においても同じです。
サブの20が確保できている会社はそう多くないと思いますが課長や部長等、リーダーが20(20/80=25%)、作業員60(60/80=75%)には大体なっていますよね。
では「あと会社に足りないのは?」といった考えを生じさせます。
会社だけでなく組織やスポーツチームを作る際も効率的で効果的なのは「20:60:20」を片隅に置いておくと役立つかもしれません。
※これ実は本当に働かないアリもいてそのアリが増殖して組織を崩壊させることがあります(笑)
※アリ社会も複雑怪奇ですね・・・
3:10:60:27
ハーバード大学が検証した人の行動を表したものです。
これも聞いたことがある人は多いと思います。
分かりやすくすると、
学校の先生が生徒たちに「ここテスト出るから覚えてね」と授業中に言ったとします。

3:そもそも勉強済みであり既に覚えている いわゆる天才・大成功する人
10:先生に言われたことを守り行動・努力する 努力して成功する人
60:確かにテストに出ることは聞いたけどやらない 知ってはいるが行動しない人
27:そもそも話を聞いていない 知らないし知りたいとも思わない人
教室に何人いるかは分かりませんが多ければ多いほどこの割合で分かれます。
これもパレートの法則のようにほとんど事象に当てはめる事が出来ます。
例えば商売に応用すれば、
「サービスを提供する側13:サービスを受ける側87」に分けられたり、
もっと細かく、営業の観点で新商品を売る際で考えると
新しいものは営業されなくても買う:3
新しいものに興味があり、説明を聞いて買う:10
ひとが買うのを見て買う:60
新しいものに抵抗があるし買わない:27
と考え、「じゃあ83の人は見込み客だよね!売れるよね!」という脅し文句に使われたり(笑)
簡単に、
「成功する人13:成功しない人87」のように使われ、「一緒に成功する13の人間、いや大成功する3の人間になりましょう!」というように怪しい宗教の勧誘に使われたり(笑)します。
それだけ様々なシーンで使われ、人々も納得して聞き入れてしまう「3:10:60:27」です。
これは覚えておかないといけません。
おわりに
あまり長くなっても覚えられないと思いますので毎回3~4くらいのペースで投稿していこうかと思います。
(かなた自身が一気に書かれても覚えられないと感じたので(笑))
知識は自分を守るにも何をするにも必要です。
例えばあなたが世の中の全てを知る「全知」の存在だったとしてできないことはありますか?
全てを可能にできる知識があれば身体を順応させれば何でもできます。その方法も知っています。

まあ全知は不可能なことだと思いますがそれに少しずつでも近づいていくことはできますよね。
聞いたことがある程度でも役に立つときは立ちます。
一緒に知識を蓄えていきましょう。
ブログランキング参加してみました↓を押してもらえるとやる気がみなぎります(かなたの)
②も投稿しました。
他保険、自己啓発的な事も書いてます






